- Weekly Dose of Random Knowledge
- Posts
- Understand Topology Under 5 Minutes
Understand Topology Under 5 Minutes
Why a donut is the same as a coffee mug

Topology can be counterintuitive, especially when first learning about it. How could a donut be remotely similar to a coffee mug? Sure, they both have one hole.

the deformation from a donut to a cup is called homeomorphism.
“a topologist pours coffee into their doughnut and eats their mug.” — (haha)
In geometry, all the shapes are rigid objects; a pyramid is definitely not a sphere. But in topology, shapes are squishy and soft, like Play-Doh or rubber. And a cube is treated no differently than a pyramid or a sphere. Geometry and topology are close kin to each other, and today we will be exploring how one is born from the other.
An essential characteristics of a polyhedra are its number of faces, vertices, and edges. Take a cube for instance, it has 8 vertices, 12 edges, and 6 faces. A tetrahedron (3D triangle) has 4 vertices, 6 edges, and 4 faces.
Leonhard Euler noticed in 1750 that if there are F faces, E edges, and V vertices, then V-E+F=2. For a cube, 8-12+6=2; for a tetrahedron, 4-6+4=2. This pattern applies to all polyhedrons. Such a simple observation revealed another dimension of mathematics: this result doesn’t depend on the geometric properties of the shape, but on its topological features.
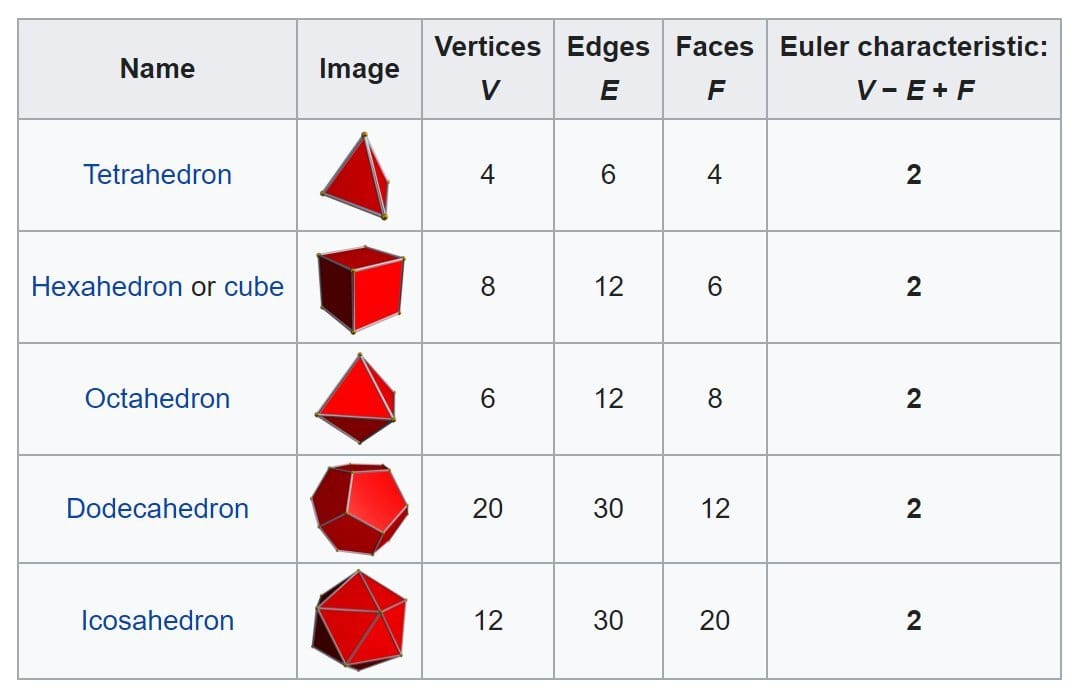
What Euler observed was called the Euler Characteristics. We can say, the Euler Characteristic of all the polyhedrons above is 2.
Can we find examples of shapes with an Euler Characteristic that’s not two? Well, what mathematicians found was that the Euler Characteristic is two only when it’s a convex polyhedron, meaning the line segment joining any two points drawn on the surface of the polyhedron lies inside the polyhedron.
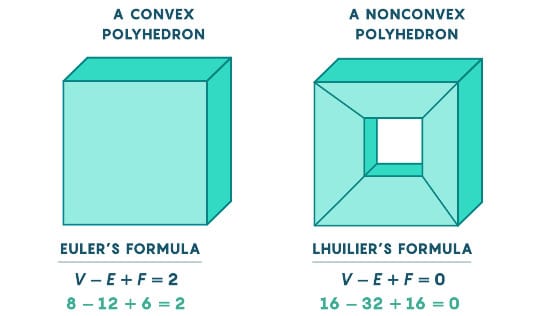
Convex polyhedron vs nonconvex Polyhedron
When looking at a nonconvex polyhedron, its Euler Characteristic could be 0 or -2. We notice when Euler Characteristic varies, the number of holes in an object varies. Here we need to clarify that holes in topology refer to 1) a through hole like a straw or 2) a buried hole like what cheese has. A blind hole such as a teeth cavity isn’t considered a hole in topology.
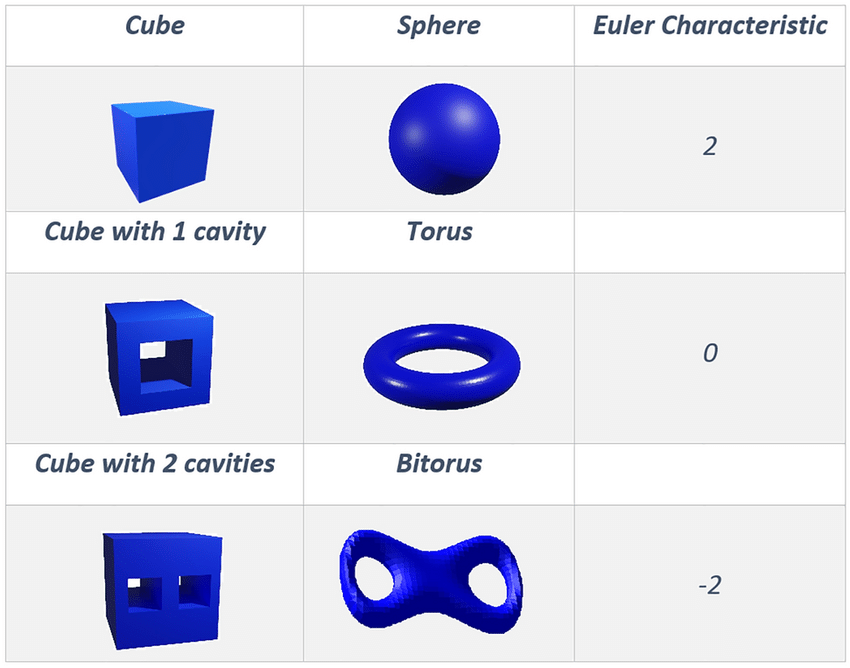
What we also notice here is that the specific shape doesn’t affect the Euler Characteristic, only the number of holes does.
We briefly mentioned homeomorphism earlier. If you have a shape made out of Play-Doh, the process of morphing this shape into another without gluing the surface is basically homeomorphism. In formal terms, homeomorphism is a continuous one-to-one mapping of two geometric shapes.
Two shapes that are homomorphic to each other is considered the same becasue they share the same topological features. And how you determine if two shapes are homeomorphic is through its Euler Characteristic. Thus, two shapes are homeomorphic if and only if they share an Euler Characteristic.
Now you know why a donut is the same as a coffee mug to a topologist!
Thank you for reading my weekly newsletter, I hope it was interesting to you. I’m open to all kinds of feedback so please email me if you have any. Remember to let me know if you have a request. If you enjoyed this article, please share it with your friends!